Billionaires wanted it, but 66,930 everyday investors got it first.
When incredibly valuable assets come up for sale, it's typically the wealthiest people that end up taking home an amazing investment. But not always…
One platform is taking on the billionaires at their own game, buying up and securitizing some of the most prized blue-chip artworks for its investors.
It's called Masterworks. Their nearly $1 billion collection includes works by greats like Banksy, Picasso, and Basquiat. When Masterworks sells a painting – like the 23 it's already sold – investors reap their portion of the net proceeds.
In just the last few years, Masterworks investors have realized net annualized returns like +17.6%, +17.8%, and +21.5% (from 3 illustrative sales held longer than one year).
Past performance not indicative of future returns. Investing Involves Risk. See Important Disclosures at masterworks.com/cd.
Exciting News: Paid Subscriptions Have Launched! 🚀
On September 1, we officially rolled out our new paid subscription plans at GuruFinance Insights, offering you the chance to take your investing journey to the next level! Whether you're just starting or are a seasoned trader, these plans are packed with exclusive trading strategies, in-depth research paper analysis, ad-free content, monthly AMAsessions, coding tutorials for automating trading strategies, and much more.
Our three tailored plans—Starter Investor, Pro Trader, and Elite Investor—provide a range of valuable tools and personalized support to suit different needs and goals. Don’t miss this opportunity to get real-time trade alerts, access to masterclasses, one-on-one strategy consultations, and be part of our private community group. Click here to explore the plans and see how becoming a premium member can elevate your investment strategy!

1. Introduction
Forecasting financial markets is a sophisticated fusion of quantitative precision and global economic nuance. In this quest, the Monte Carlo simulation stands out as a premier statistical instrument, guiding our understanding of future stock prices.
Named after the famous Monte Carlo Casino in Monaco, this method doesn’t bank on luck but is rooted in rigorous probabilistic modelling. Imagine orchestrating thousands of experiments in a controlled environment, with each one unfolding a different story of stock price movement. That’s the power of the Monte Carlo simulation. It allows us to visualize a spectrum of outcomes based on historical data and probabilistic assumptions.
In this article, our approach is twofold: First, we delve into the intricacies of historical and implied volatilities, elucidating their distinctions, implications, and relevance. While historical volatility gauges the fluctuations of past stock prices, implied volatility offers a forward-looking perspective based on market sentiments and option pricing. Next, we employ the Monte Carlo simulation, using both these volatility measures, to extrapolate potential future paths for our chosen stock.
Central to our analysis will be the derivation of probabilities. By observing the simulation’s multitude of potential outcomes, we’ll compute the likelihood of the stock price landing within specific ranges. For instance, what’s the probability of the stock price exceeding a particular threshold or falling below another? Therefore, offering a quantifiable perspective on potential future scenarios.
2. Volatility Analysis
2.1 Historical Volatility
Historical volatility, often termed statistical or realized volatility, quantifies the variability of a stock’s returns over a past period. It gives us an idea of how much a stock’s price deviated from its average value during that timeframe.
Once you have the daily returns, the historical volatility (HV) over N days is calculated as

Formula illustrating the computation of daily historical volatility. The calculation is based on returns of stock prices and provides a measure of how much the stock has fluctuated on a day-to-day basis in the past.
Where:
ˉRˉ = Average daily return over the N days
To convert daily volatility to annualized volatility you can use the formula below. This formula is key when you want to estimate volatility over a given horizon.
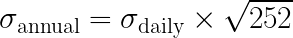
Formula for converting daily historical volatility to annualized volatility. The transformation incorporates the square root of the number of trading days in a year (typically 252), offering a more long-term perspective on stock price fluctuations.
2.2 Implied Volatility
The implied volatility can be extracted from the Black-Scholes option pricing model:

Black-Scholes-Merton formula for pricing European call options. The formula establishes the theoretical value of an option by accounting for factors such as stock price, exercise price, time to maturity, implied volatility, and the risk-free rate.
Where:
C is the call option price.
S0 is the current stock price.
X is the strike price of the option.
t is the time to expiration.
r is the risk-free rate.
q is the dividend yield.
N() is the CDF of the standard normal distribution.

Formula for d1 in the Black-Scholes-Merton option pricing model. d1 captures the expected price movements of the underlying stock relative to the option strike price and is a determinant factor in option valuation.

Formula for d2 in the Black-Scholes-Merton option pricing model. d2 is derived from d1 and represents the probability that an option will be exercised given its current pricing and other influencing factors.
It’s worth noting that although the above describes the derivation for a call option, a similar approach is taken for put options. To extract implied volatility (σ), one would reverse engineer the model using the observed market option price.
However, the process can be computationally intensive, especially for those unfamiliar with the nuances of option pricing models. As a result, many traders and investors prefer sourcing the implied volatility value directly from platforms like Yahoo Finance or their trading brokers.
2.3 Historical vs. Implied Volatility
Historical and implied volatilities, though related, serve different purposes:
Perspective: While historical volatility looks backward, gauging price fluctuations from past data, implied volatility peers forward, encapsulating market expectations of future price variability.
Application: Historical volatility aids in risk assessment based on past stock behavior. In contrast, implied volatility is pivotal for options pricing and understanding market sentiment about future volatility.
Determination: Historical volatility is purely statistical, derived from past price data. Implied volatility, however, is extracted from the market prices of options, embodying the collective wisdom of market participants.
3. Monte Carlo Simulations for Price Forecasting
The Monte Carlo simulation leverages probability theory to determine possible outcomes for an uncertain event. In finance, it offers a method to model the evolution of stock prices, based on certain statistical characteristics, primarily the volatility.
3.1 Drift and Volatility
The main components determining stock price movements in our simulation are the drift and the volatility. The drift represents the expected or average rate of return of a stock, adjusted for the time frame of the forecast.

Formula illustrating the drift component in the geometric Brownian motion model. This component represents the expected rate of return on the stock, accounting for inherent factors over the forecast period.
Where:
μ is the expected stock return.
σ2 is the variance (volatility squared).
Δt is the time increment.
Volatility, on the other hand, accounts for the unpredictability and brings randomness into our forecast:

Equation capturing the volatility term in the geometric Brownian motion model. This element introduces randomness to the forecast, representing the inherent unpredictability and risk of stock movements.
Where:
ϵ is a random value drawn from a standard normal distribution.
3.2 Stock Price Path Simulation
To simulate the path of stock prices, we apply the following recursive formula:

Recursive formula showcasing the stock price path simulation. With the initial stock price S0, this equation combines the drift and volatility to project future stock prices S1,S2,….
Starting from the initial stock price S0, we compute successive prices S1,S2,… using the drift, the volatility term, and the previous stock price.
3.3 Stock Price Path Simulation
The power of the Monte Carlo method emerges when running thousands or even millions of simulations. Each trajectory will offer a unique path for the stock price based on the randomness injected by the volatility term. Collectively, they provide a spectrum of possible outcomes, shaping a probability distribution for future stock prices.
3.4 Stock Price Path Simulation
After obtaining a multitude of stock price paths, we can perform various statistical analyses. For instance, calculating the mean and variance provides insights into the central tendency and dispersion of our forecasts. Moreover, by examining the distribution of the final stock prices from all simulations, we can compute probabilities for the stock landing within certain ranges, as previously discussed.
In conclusion, the Monte Carlo simulation offers a dynamic and probabilistic approach to stock price forecasting. While no model can predict the future with certainty, this method provides a robust framework for understanding potential price trajectories and their associated probabilities.
4. Implementation of Monte Carlo Simulation
In this section, we outline the steps and methodologies used to conduct the previously analyses discussed on Volatility and Monte Carlo.
4.1 Methodology Overview
The simulation uses the Geometric Brownian Motion model, a widely recognized model for stock price dynamics, primarily influenced by drift (deterministic) and volatility (stochastic).
4.2 Data Collection
To begin our simulation, we source the stock’s historical data:
import yfinance as yf
# Download historical data for ASML.AS
symbol = "ASML.AS"
start_date = "2020-01-01"
end_date = "2023-12-30"
df = yf.download(symbol, start=start_date, end=end_date)4.3 Computing Daily Returns
With the historical data in place, we compute the stock’s daily returns, serving as the foundation for our simulation:
import numpy as np
# Calculate daily returns
log_returns = np.log(df['Close'] / df['Close'].shift(1))4.4 Monte Carlo Simulation Setup
Before the simulation starts, we specify key parameters, guiding the forecast’s trajectory:
# Monte Carlo simulation parameters
days_to_forecast = 20
num_simulations = 10000
dt = 1 # 1 trading day4.5 Volatility Inclusion
Implied volatility is introduced, based on our earlier discussions in the volatility section:
# Volatility for BSM
volatility_bsm = 0.29 # Assuming 29% annualized volatility
print("BMS Implied Volatility: ", volatility_bsm)4.6 Running the Simulations
Leveraging the calculated logarithmic returns and assumed implied volatility, we create two sets of simulations:
from scipy.stats import norm
# Function to run the Monte Carlo simulation
def run_simulation(volatility, dt, annualized=False):
...
# simulation logic here
...
simulated_prices_historical = run_simulation(log_returns.std(), dt)
simulated_prices_bsm = run_simulation(volatility_bsm, dt, annualized=True)
print("Historical Volatility: ", log_returns.std())4.7 Visualization
The results are visualized through the Monte Carlo confidence cones, showcasing the possible stock price trajectories under both the historical and BSM volatility:
import matplotlib.pyplot as plt
# Plotting logic
fig, axs = plt.subplots(1, 2, figsize=(30, 7))
...
# rest of the plotting logic
plt.show()This visualization provides a detailed look at potential price paths using two different volatility measures. By overlaying these paths with specified thresholds and confidence intervals, investors can derive meaningful insights into potential future stock movements.
4.8 Understanding Key Parameters
Thresholds:
In the code, we’ve identified two important thresholds for the stock prices. These thresholds might represent critical resistance or support levels from a technical analysis perspective or specific price levels of interest to the investor.
# Define thresholds
threshold1 = 650 #Upper Threshold
threshold2 = 540 #Lower Threshold4.9 Derived Probabilities
From the simulation results, we can calculate the probabilities of the stock price being above threshold1, below threshold2, and between the two thresholds at the end of our forecast period:
# Probability annotations
above_threshold1_prob = (simulated_prices[-1] > threshold1).sum() / num_simulations
below_threshold2_prob = (simulated_prices[-1] < threshold2).sum() / num_simulations
between_thresholds_prob = 1 - above_threshold1_prob - below_threshold2_probThese probabilities provide valuable insights:
The likelihood that the stock price exceeds a favorable price level (above
threshold1).The risk of the stock price dropping below a concerning level (
threshold2).The probability that the stock price remains between these two thresholds.
Putting it all together:
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
from scipy.stats import norm
# Download historical data for ASML.AS
symbol = "ASML.AS"
start_date = "2020-01-01"
end_date = "2023-12-30"
df = yf.download(symbol, start=start_date, end=end_date)
# Calculate daily returns
log_returns = np.log(df['Close'] / df['Close'].shift(1))
# Monte Carlo simulation parameters
days_to_forecast = 20
num_simulations = 10000
dt = 1 # 1 trading day
# Define thresholds
threshold2 = 540 #144 #116
threshold1 = 650 #162 #128
# Volatility for BSM
volatility_bsm = 0.29 # Assuming 29% annualized volatility
print("BMS Implied Volatility: ", volatility_bsm)
# Run Monte Carlo simulations
def run_simulation(volatility, dt, annualized=False):
simulated_prices = np.zeros((days_to_forecast, num_simulations))
simulated_prices[0] = df['Close'][-1]
# Adjust volatility for annualized estimates
if annualized:
volatility = volatility / np.sqrt(252)
for t in range(1, days_to_forecast):
random_walk = np.random.normal(loc=log_returns.mean() * dt,
scale=volatility * np.sqrt(dt),
size=num_simulations)
simulated_prices[t] = simulated_prices[t - 1] * np.exp(random_walk)
return simulated_prices
simulated_prices_historical = run_simulation(log_returns.std(), dt)
simulated_prices_bsm = run_simulation(volatility_bsm, dt, annualized=True)
print("Historical Volatility: ", log_returns.std())
# Plot the results
fig, axs = plt.subplots(1, 2, figsize=(30, 7))
for simulated_prices, ax, title in zip([simulated_prices_historical, simulated_prices_bsm], axs, ['Historical Volatility', 'BSM Volatility']):
mean_price_path = np.mean(simulated_prices, axis=1)
median_price_path = np.median(simulated_prices, axis=1)
lower_bound_68 = np.percentile(simulated_prices, 16, axis=1)
upper_bound_68 = np.percentile(simulated_prices, 84, axis=1)
lower_bound_95 = np.percentile(simulated_prices, 2.5, axis=1)
upper_bound_95 = np.percentile(simulated_prices, 97.5, axis=1)
# Define thresholds
threshold1 = threshold1
threshold2 = threshold2
ax.plot(simulated_prices, color='lightgray', alpha=0.1)
ax.plot(mean_price_path, color='black', label='Mean Price Path')
ax.plot(median_price_path, color='blue', label='Median Price Path')
ax.plot(lower_bound_68, color='green', linestyle='--', label='68% confidence interval (Lower)')
ax.plot(upper_bound_68, color='green', linestyle='--', label='68% confidence interval (Upper)')
ax.plot(lower_bound_95, color='blue', linestyle='--', label='95% confidence interval (Lower)')
ax.plot(upper_bound_95, color='red', linestyle='--', label='95% confidence interval (Upper)')
ax.axhline(y=threshold1, color='purple', linestyle='--', alpha=0.25, label='Threshold 1')
ax.axhline(y=threshold2, color='orange', linestyle='--', alpha=0.25, label='Threshold 2')
# Plot settings
ax.set_xlabel('Days')
ax.set_ylabel('Stock Price')
ax.set_title(f'Monte Carlo Confidence Cone for {symbol} using {title}', fontsize = 25)
ax.legend(fontsize = 15)
# Add price estimates every 5 days
for day in range(0, days_to_forecast, 5):
ax.annotate(f'{lower_bound_68[day]:.2f}', xy=(day, lower_bound_68[day]), xycoords='data',
xytext=(-50, 0), textcoords='offset points', color='green')
ax.annotate(f'{upper_bound_68[day]:.2f}', xy=(day, upper_bound_68[day]), xycoords='data',
xytext=(-50, 0), textcoords='offset points', color='green')
ax.annotate(f'{lower_bound_95[day]:.2f}', xy=(day, lower_bound_95[day]), xycoords='data',
xytext=(-50, 0), textcoords='offset points', color='blue')
ax.annotate(f'{upper_bound_95[day]:.2f}', xy=(day, upper_bound_95[day]), xycoords='data',
xytext=(-50, 0), textcoords='offset points', color='red')
# Add probability annotations
above_threshold1_prob = (simulated_prices[-1] > threshold1).sum() / num_simulations
below_threshold2_prob = (simulated_prices[-1] < threshold2).sum() / num_simulations
between_thresholds_prob = 1 - above_threshold1_prob - below_threshold2_prob
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
ax.text(0.02, 0.05, f'P(>{threshold1:.2f}): {above_threshold1_prob:.2%}\n'
f'P(<{threshold2:.2f}): {below_threshold2_prob:.2%}\n'
f'P({threshold2:.2f} - {threshold1:.2f}): {between_thresholds_prob:.2%}',
transform=ax.transAxes, fontsize=15,
verticalalignment='bottom', bbox=props)
# Add mean price path labels
#ax.annotate(f'{mean_price_path[-1]:.2f}', xy=(days_to_forecast - 1, mean_price_path[-1]), xycoords='data',
# xytext=(15, 0), textcoords='offset points', color='black')
# Add median price path labels
ax.annotate(f'{median_price_path[-1]:.2f}', xy=(days_to_forecast - 1, median_price_path[-1]), xycoords='data',
xytext=(15, 0), textcoords='offset points', color='blue')
# Add price labels
ax.annotate(f'{lower_bound_68[-1]:.2f}', xy=(days_to_forecast - 1, lower_bound_68[-1]), xycoords='data',
xytext=(-15, 0), textcoords='offset points', color='green')
ax.annotate(f'{upper_bound_68[-1]:.2f}', xy=(days_to_forecast - 1, upper_bound_68[-1]), xycoords='data',
xytext=(-15, 0), textcoords='offset points', color='green')
ax.annotate(f'{lower_bound_95[-1]:.2f}', xy=(days_to_forecast - 1, lower_bound_95[-1]), xycoords='data',
xytext=(-15, 0), textcoords='offset points', color='blue')
ax.annotate(f'{upper_bound_95[-1]:.2f}', xy=(days_to_forecast - 1, upper_bound_95[-1]), xycoords='data',
xytext=(-15, 0), textcoords='offset points', color='red')
plt.show()
Monte Carlo Simulations of ASML.AS Stock Trajectories: An Examination of Historical vs. BSM Implied Volatilities and Their Respective Probabilistic Outcomes Over a 20-Day Forecast Horizon.
4.10 Historical vs. Implied Volatility: Results Comparison
Our simulation provided two sets of potential future stock price paths, one based on historical volatility and the other on implied volatility. Here’s a brief comparison:
Historical Volatility: Derived from the stock’s past price movements, our simulation gives us a projection rooted in its historical behavior. In environments where market conditions remain consistent, this could offer a reliable forecast.
BSM Implied Volatility: This represents market expectations. In scenarios where there are anticipated future events or changes in market conditions, the implied volatility may provide a more relevant projection.
By comparing these two simulations, we gain a more comprehensive perspective:
If both simulations align closely, it indicates a consensus between past behavior and market expectations.
Divergence between the two suggests that there are external factors or market expectations not captured by the historical data.
The side-by-side visual representation in the plots further illustrates these dynamics, providing a robust tool for investors to weigh the potential risks and rewards.
5. Concluding Remarks
Financial market dynamics are complex, oscillating between historical trends and ever-evolving market sentiments. Our Monte Carlo simulation, leveraging both historical and implied volatility, offers a rich tapestry of potential outcomes for the stock prices . But like all models, its strength lies not just in the predictions it renders but also in the insights it offers.
Appreciating Uncertainty: One of the most salient takeaways from our analysis is the range of potential outcomes. This range encapsulates the inherent uncertainty in stock price movements, emphasizing the need for risk management.
Informed Decision Making: The simulation offers a a spectrum of possibilities. Investors can use these insights to inform their decisions, whether it’s setting stop-loss orders, determining entry and exit points, or simply adjusting their portfolio’s risk profile.
The Importance of Both Historical and Implied Volatilities: Our analysis underlined the significance of considering both past stock movements and market sentiments. While the historical data offers a look into how the stock behaved under past market conditions, implied volatility provides a window into market expectations. By juxtaposing these two, investors can capture a more holistic view of potential stock movements.
In conclusion, tools like the Monte Carlo simulation empower investors to peer into a range of potential tomorrows. It’s a step away from mere speculation and a leap towards informed, data-driven decision-making



