Getting Started with Itô’s Lemma for Stochastic Finance

Where Accomplished Wealth Builders Connect, Learn & Grow

Long Angle is a private, vetted community for high-net-worth entrepreneurs and executives. No fees, no pitches—just real peers navigating wealth at your level. Inside, you’ll find:

• Self-made professionals, 30–55, $5M–$100M net worth

• Confidential conversations, peer advisory groups, live meetups

• Institutional-grade investments, $100M+ deployed annually

Apply to Join

🚀 Your Investing Journey Just Got Better: Premium Subscriptions Are Here! 🚀

It’s been 4 months since we launched our premium subscription plans at GuruFinance Insights, and the results have been phenomenal! Now, we’re making it even better for you to take your investing game to the next level. Whether you’re just starting out or you’re a seasoned trader, our updated plans are designed to give you the tools, insights, and support you need to succeed.

Here’s what you’ll get as a premium member:

• Exclusive Trading Strategies: Unlock proven methods to maximize your returns.

• In-Depth Research Analysis: Stay ahead with insights from the latest market trends.

• Ad-Free Experience: Focus on what matters most—your investments.

• Monthly AMA Sessions: Get your questions answered by top industry experts.

• Coding Tutorials: Learn how to automate your trading strategies like a pro.

• Masterclasses & One-on-One Consultations: Elevate your skills with personalized guidance.

Our three tailored plans—Starter Investor, Pro Trader, and Elite Investor—are designed to fit your unique needs and goals. Whether you’re looking for foundational tools or advanced strategies, we’ve got you covered.

Don’t wait any longer to transform your investment strategy. The last 4 months have shown just how powerful these tools can be—now it’s your turn to experience the difference.

👉 Explore Premium Plans Now

Wall Street has Bloomberg. You have Stocks & Income.

Why spend $25K on a Bloomberg Terminal when 5 minutes reading Stocks & Income gives you institutional-quality insights?

We deliver breaking market news, key data, AI-driven stock picks, and actionable trends—for free.

Subscribe for free and take the first step towards growing your passive income streams and your net worth today.

Get Free Daily Market Updates →

_{Stocks & Income is for informational purposes only and is not intended to be used as investment advice. Do your own research.}

Stochastic calculus gives us the tools to work with randomness in motion. Classic calculus fails when the underlying variable follows a Brownian path. With Itô’s Lemma and its extensions, we analyze asset prices, derive dynamics, and simulate outcomes under uncertainty. Let’s look at Itô’s Lemma and examine how we apply them to equities and interest rates.

Let X_t follow an Itô process:

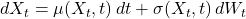
This handles a single process. Most practical models involve multiple variables. For two stochastic processes Xt and Yt, each with its own drift, volatility, and a possible correlation ρ. Brownian motion has infinite variation. That makes Itô calculus a second-order theory, unlike classical first-order differentials.

Applications in Equities and Interest Rates

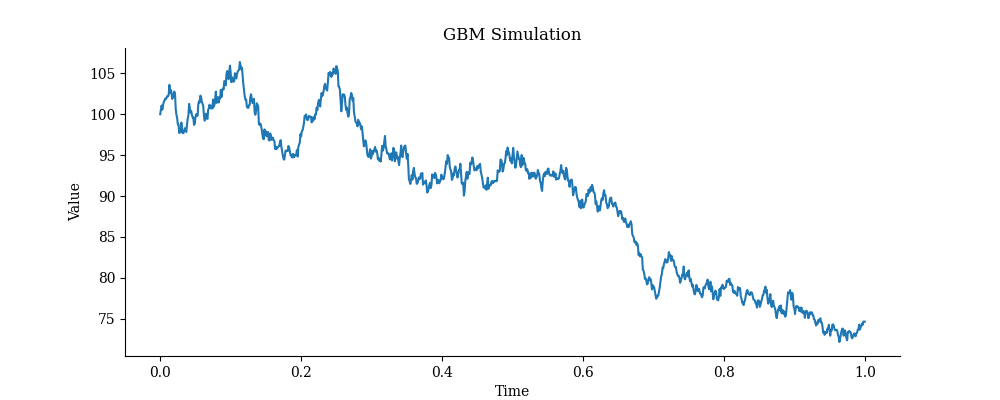
Let S_t be an equity price following geometric Brownian motion:

Apply Itô’s Lemma to ln⁡(S_t):

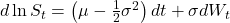
This result shows that log returns are normally distributed. It also allows us to simulate S_t directly:

This forms the basis for derivative pricing and portfolio modeling.

Interest rate models often use mean-reverting processes. A common form is the Ornstein-Uhlenbeck process:

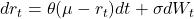
Apply Itô’s Lemma to f(r_t) = r_t², and you get a dynamic for the variance. Apply it to bond prices P(t, T), and you get the PDE governing fixed-income instruments. These dynamics shape yield curves and forward rates.

Retirement Planning Made Easy

Building a retirement plan can be tricky— with so many considerations it’s hard to know where to start. That’s why we’ve put together The 15-Minute Retirement Plan to help investors with $1 million+ create a path forward and navigate important financial decisions in retirement.

Get your free guide today.

Generating Standard Normal Random Variables

Simulating stochastic processes begins with normal random variables. To simulate Brownian motion, we draw:

Then construct an increment ΔW over a small time step Δt as:

This allows numerical schemes such as Euler-Maruyama:

By simulating thousands of paths, we approximate expectations under stochastic models. This is the basic concept behind Monte Carlo simulation.

The Steady State Distribution

Some stochastic processes settle into a stable distribution. These processes are called ergodic. Over time, they forget their initial state.

The Ornstein-Uhlenbeck process gives us:

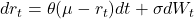
As t→∞, the distribution of r_t approaches:

This is the steady state. It gives insight into the long-run behavior of interest rates or volatility.

If a process lacks a steady state (like geometric Brownian motion), the variance grows with time. That reflects unbounded uncertainty. If a process has a steady state, its risk is contained.

Steady states guide portfolio construction and scenario analysis. They help quantify long-run expectations and define convergence targets in simulation.

Stochastic calculus extends classical tools into a world ruled by uncertainty. Itô’s Lemma and its extensions allow precise modeling of returns, rates, and risk. We produce standard normal draws to simulate paths. We study long-run behavior through steady state distributions.

The formulas matter, but the insight matters more. Every derivative model, every Monte Carlo path, every hedging ratio starts with this calculus. To work with financial motion, you must learn to work with noise. And noise, it turns out, has structure.

import numpy as np
import matplotlib.pyplot as plt

# Set up consistent matplotlib style
plt.rcParams.update({
    "font.family": "serif",
    "axes.spines.top": False,
    "axes.spines.right": False
})

# Ito's Lemma for log(S)
def ito_log_gbm(S0, mu, sigma, T, steps):
    dt = T / steps
    t = np.linspace(0, T, steps + 1)
    W = np.cumsum(np.random.normal(0, np.sqrt(dt), size=steps))
    W = np.insert(W, 0, 0)
    ln_S = np.log(S0) + (mu - 0.5 * sigma**2) * t + sigma * W
    S = np.exp(ln_S)
    return t, S, ln_S

# Simulate Ornstein-Uhlenbeck process
def simulate_ou(r0, mu, theta, sigma, T, steps):
    dt = T / steps
    r = np.zeros(steps + 1)
    r[0] = r0
    for i in range(steps):
        dr = theta * (mu - r[i]) * dt + sigma * np.sqrt(dt) * np.random.normal()
        r[i+1] = r[i] + dr
    return np.linspace(0, T, steps + 1), r

# Generate standard normal from Brownian increment
def simulate_standard_normal_from_bm(T, steps):
    dt = T / steps
    dW = np.random.normal(0, np.sqrt(dt), size=steps)
    Z = dW / np.sqrt(dt)  # Standardized to N(0,1)
    return Z

# Steady-state distribution for OU
def steady_state_ou_pdf(x, mu, theta, sigma):
    var = sigma**2 / (2 * theta)
    return (1 / np.sqrt(2 * np.pi * var)) * np.exp(-(x - mu)**2 / (2 * var))

# Simulate GBM and log-returns using Ito
t, S, ln_S = ito_log_gbm(S0=100, mu=0.05, sigma=0.2, T=1, steps=1000)

plt.figure(figsize=(10, 4))
plt.plot(t, S, label="GBM Price")
plt.title("GBM Simulation")
plt.xlabel("Time")
plt.ylabel("Value")
plt.savefig("ito_gbm_logprice.png")
plt.show()

# Simulate Ornstein-Uhlenbeck Process
t_ou, r = simulate_ou(r0=0.03, mu=0.05, theta=0.7, sigma=0.02, T=5, steps=1000)

plt.figure(figsize=(10, 4))
plt.plot(t_ou, r, label="OU Process (Interest Rate)")
plt.title("Ornstein-Uhlenbeck Simulation")
plt.xlabel("Time")
plt.ylabel("Rate")
plt.savefig("ou_process.png")
plt.show()

# Generate and plot standard normal
Z = simulate_standard_normal_from_bm(T=1, steps=10000)

plt.figure(figsize=(10, 4))
plt.hist(Z, bins=50, density=True, alpha=0.6, label="Simulated Standard Normals")
x = np.linspace(-4, 4, 200)
plt.plot(x, (1/np.sqrt(2*np.pi)) * np.exp(-x**2 / 2), label="PDF N(0,1)", linestyle='--')
plt.title("Standard Normal from Brownian Increments")
plt.xlabel("Z")
plt.ylabel("Density")
plt.savefig("standard_normal.png")
plt.show()

# Plot steady-state distribution
x_vals = np.linspace(-0.02, 0.10, 300)
pdf_vals = steady_state_ou_pdf(x_vals, mu=0.05, theta=0.7, sigma=0.02)

plt.figure(figsize=(10, 4))
plt.plot(x_vals, pdf_vals, label="Steady-State PDF")
plt.title("Steady-State Distribution of OU Process")
plt.xlabel("Rate")
plt.ylabel("Density")
plt.savefig("ou_steady_state.png")
plt.show()