Tackle your credit card debt by paying 0% interest until 2026

If you have outstanding credit card debt, getting a new 0% intro APR credit card could help ease the pressure while you pay down your balances. Our credit card experts identified top credit cards that are perfect for anyone looking to pay down debt and not add to it! Click through to see what all the hype is about.

Learn How To Apply Now

Exciting News: Paid Subscriptions Have Launched! 🚀

On September 1, we officially rolled out our new paid subscription plans at GuruFinance Insights, offering you the chance to take your investing journey to the next level! Whether you're just starting or are a seasoned trader, these plans are packed with exclusive trading strategies, in-depth research paper analysis, ad-free content, monthly AMAsessions, coding tutorials for automating trading strategies, and much more.

Our three tailored plans—Starter Investor, Pro Trader, and Elite Investor—provide a range of valuable tools and personalized support to suit different needs and goals. Don’t miss this opportunity to get real-time trade alerts, access to masterclasses, one-on-one strategy consultations, and be part of our private community group. Click here to explore the plans and see how becoming a premium member can elevate your investment strategy!

Check Out Latest Premium Articles

In this guide, we’ll explore how to effectively implement a momentum trading strategy. We’ll cover setting up trading signals, executing trades, and optimizing the timeframes for making the best possible trades.

The code for this implementation can be accessed here: [GitHub Link].

Key Objectives

This tutorial aims to teach the following concepts:

1. Fundamental usage of Python classes.

2. Generating and plotting trading signals.

3. Evaluating performance metrics.

4. Optimizing momentum signals for improved outcomes.

Our Goal

We’ll establish a strategy that uses a Simple Moving Average (SMA) as a trading indicator:

• Entry Signal: Buy when the price moves above the SMA.

• Exit Signal: Close the position when the price falls below the SMA.

Our goal is to identify the optimal SMA period that maximizes performance.

Setting Up the Class

The first step involves creating a class to implement the momentum strategy. This class will handle:

1. Input data (closing prices).

2. The number of days for calculating the moving average.

3. Initial investment capital.

4. Transaction cost as a percentage of trade value.

class MomentumStrategy:
    def __init__(self, price_data, moving_avg_days, starting_capital, transaction_fee):
        """
        Initialize the momentum strategy class.

        Args:
        price_data (iterable): Historical price data, expected as a list or array.
        moving_avg_days (int): The number of days for calculating the moving average.
        starting_capital (float): Initial amount of money available for trading.
        transaction_fee (float): Fee as a fraction of the trade value (e.g., 0.001 for 0.1%).
        """
        self.price_data = pd.DataFrame(price_data, columns=["Close"])
        self.moving_avg_days = moving_avg_days
        self.starting_capital = starting_capital
        self.transaction_fee = transaction_fee

    def calculate_moving_average(self):
        """
        Computes the Simple Moving Average (SMA) over the specified number of days.

        Returns:
        pd.Series: The SMA, with missing values replaced by the same day's closing price.
        """
        return self.price_data["Close"].rolling(window=self.moving_avg_days).mean().fillna(self.price_data["Close"])

Key Notes:

• The moving average is calculated using the rolling method.

• If the SMA isn’t defined (early periods without enough data), missing values are replaced with the same day's closing price to avoid invalid trades.

Next, we implement the core trading functionality:

def execute_trades(self):
        """
        Executes trades based on the momentum strategy and tracks key metrics.

        Process:
        - Compute the SMA and compare it with the closing prices.
        - Mark when to enter or exit a trade using signals (1 for buy, -1 for sell).
        - Maintain records for current position value, shares held, transaction costs, cash, and overall portfolio value.
        """
        # Add the moving average to the dataset
        self.price_data["SMA"] = self.calculate_moving_average()

        # Define signals: 1 for buy, -1 for sell, and 0 for no action
        self.price_data["Signal"] = (self.price_data["Close"] > self.price_data["SMA"]).astype(int).diff().fillna(0)

        # Initialize columns for portfolio tracking
        self.price_data["PositionValue"] = 0.0  # Value of held shares
        self.price_data["SharesHeld"] = 0  # Number of shares currently held
        self.price_data["TransactionCosts"] = 0.0  # Total transaction costs incurred
        self.price_data["AvailableCash"] = self.starting_capital  # Cash available for trading
        self.price_data["PortfolioValue"] = self.starting_capital  # Total value of the portfolio

        # Iterate through the data to update portfolio values
        for i in range(len(self.price_data)):
            if self.price_data.loc[i, "Signal"] == 1:  # Buy signal
                shares_to_buy = self.price_data.loc[i, "AvailableCash"] // self.price_data.loc[i, "Close"]
                cost = shares_to_buy * self.price_data.loc[i, "Close"] * (1 + self.transaction_fee)
                self.price_data.loc[i, "SharesHeld"] = shares_to_buy
                self.price_data.loc[i, "TransactionCosts"] += cost
                self.price_data.loc[i, "AvailableCash"] -= cost

            elif self.price_data.loc[i, "Signal"] == -1:  # Sell signal
                sell_value = self.price_data.loc[i - 1, "SharesHeld"] * self.price_data.loc[i, "Close"] * (1 - self.transaction_fee)
                self.price_data.loc[i, "SharesHeld"] = 0
                self.price_data.loc[i, "AvailableCash"] += sell_value
                self.price_data.loc[i, "TransactionCosts"] += sell_value * self.transaction_fee

            # Update position and total portfolio value
            self.price_data.loc[i, "PositionValue"] = self.price_data.loc[i, "SharesHeld"] * self.price_data.loc[i, "Close"]
            self.price_data.loc[i, "PortfolioValue"] = self.price_data.loc[i, "PositionValue"] + self.price_data.loc[i, "AvailableCash"]

        # Calculate benchmark and strategy returns
        self.price_data["BenchmarkReturns"] = self.price_data["Close"].pct_change().fillna(0)
        self.price_data["StrategyReturns"] = self.price_data["PortfolioValue"].pct_change().fillna(0)Key Points:

1. Signals identify whether to enter (1) or exit (-1) positions.

2. Portfolio Metrics:

• Track cash, shares held, position value, and total portfolio value after each action.

3. Transaction Costs: Applied proportionally based on trade size.

The difference in benchmark returns and strategy returns highlights the strategy’s effectiveness.

Testing the Momentum Strategy with the S&P 500 Index

To evaluate how well this momentum strategy performs, we’ll apply it to the S&P 500 Index (SPX). The data will be sourced from Yahoo Finance, covering the entire historical range since the index’s inception.

Parameters for Testing

We’ll configure the strategy with the following settings:

• Moving Average Period: 200 trading days.

• Initial Capital: $1,000,000.

• Transaction Cost: 0.1% of the trade value.

Fetching Data and Initializing the Class

First, we need to pull the historical closing prices of the S&P 500 Index:

import yfinance as yf

# Fetch SPX historical data starting from January 1928
spx_data = yf.Ticker("^GSPC")
spx_closing_prices = spx_data.history(start="1928-01-01")["Close"]

# Initialize the MomentumStrategy class
trade_strategy = MomentumStrategy(spx_closing_prices, 200, 1000000, 0.001)
trade_strategy.execute_trades()

Expected Outcome

Running this setup should produce output similar to the following, including a detailed analysis of portfolio value, signals, and returns over time. The visualization would highlight the performance of the strategy against the index, showing where the strategy outperformed the benchmark.

Plotting the Signals for the Moving Average Strategy

To visualize the trading signals generated by the strategy, we can use Matplotlib to create a combined plot. This will include:

1. Line Plots:

• The actual price of the index (closing prices).

• The Simple Moving Average (SMA).

2. Scatter Plots:

• Green upward arrows for buy signals.

• Red downward arrows for sell signals.

Code for the Signal Plot Function

def plot_signals_and_sma(self):
    """
    Visualize the trading signals and the Simple Moving Average (SMA).
    
    This function combines:
    - A line plot of the closing prices and the SMA.
    - Markers for buy signals (green upward arrows) and sell signals (red downward arrows).
    """
    # Set up the figure and axis
    plt.figure(figsize=(20, 7))

    # Plot the closing prices and the SMA
    plt.plot(self.data.index, self.data["Close"], label='Closing Price', color='blue')
    plt.plot(self.data.index, self.data["SMA"], label='Simple Moving Average (SMA)', color='orange')

    # Overlay buy and sell signals as scatter plots
    plt.scatter(self.data.index, self.data["Buy"], marker='^', color='green', label='Buy Signal', alpha=1)
    plt.scatter(self.data.index, self.data["Sell"], marker='v', color='red', label='Sell Signal', alpha=1)

    # Add chart details
    plt.title("Moving Average Trading Strategy")
    plt.xlabel("Date")
    plt.ylabel("Price")
    plt.legend()
    plt.grid()

    # Display the plot
    plt.show()

How to Use the Function

Once this function is added to your MomentumStrategy class, you can call it to generate the plot:

trade_strategy.plot_signals_and_sma()

Expected Visualization

The resulting plot should display:

• The price of the S&P 500 and the SMA trend over time.

• Green upward markers at points where buy signals were triggered.

• Red downward markers at locations of sell signals.

This allows us to clearly identify entry and exit points within the historical data.

Comparing Performance: Strategy vs. Index

To assess how the strategy stacks up against the underlying index, we can visualize their cumulative returns. Since we have already calculated the cumulative returns for both the strategy and the index, we can directly plot them.

Code for Performance Plot Function

def plot_performance_comparison(self):
    """
    Visualize the cumulative returns of the trading strategy compared to the index.
    
    This function plots:
    - The cumulative returns achieved by the trading strategy.
    - The cumulative returns of the benchmark index.
    """
    # Set up the figure and axis
    plt.figure(figsize=(20, 7))

    # Plot cumulative returns of the strategy and the index
    plt.plot(self.data.index, self.data["Cum_Returns"], label='Trading Strategy', color='blue')
    plt.plot(self.data.index, self.data["Index_Cum_Returns"], label='Index', color='orange')

    # Add chart details
    plt.title("Cumulative Returns Comparison")
    plt.xlabel("Date")
    plt.ylabel("Cumulative Return")
    plt.legend()
    plt.grid()

    # Display the plot
    plt.show()

How to Use the Function

After incorporating this function into the MomentumStrategy class, you can use it to generate the comparative plot:

trade_strategy.plot_performance_comparison()

Expected Outcome

The resulting chart will display:

• The growth of $1 based on the trading strategy’s cumulative returns over time.

• The performance of $1 invested in the benchmark index.

This enables a direct comparison of how the strategy performs relative to the market, highlighting periods of outperformance and underperformance.

Comparing Performance Using Key Metrics

To evaluate the performance of the trading strategy relative to the benchmark index, we calculate the following metrics:

1. Annualized Returns: Measures the average yearly growth of an investment.

2. Annualized Volatility: Calculates the standard deviation of returns over a year, representing risk.

3. Sharpe Ratio: A simplified metric that evaluates risk-adjusted returns by dividing annualized returns by annualized volatility. (Although traditionally, a risk-free rate is factored into the calculation, we omit it here for simplicity.)

For consistency, we use 252 trading days per year to annualize all values.

Code for Performance Metrics Calculation

def calculate_performance_metrics(self):
    """
    Compute performance metrics for the trading strategy and index.
    
    Returns:
        pd.DataFrame: A summary of the performance metrics for both the strategy and the index, 
                      including annualized returns, volatility, and Sharpe ratio.
    """
    # Extract daily returns for the strategy and the index
    strategy_returns = self.data["Returns"]
    index_returns = self.data["Index_Returns"]

    # Calculate annualized returns
    annualized_strategy_returns = (1 + strategy_returns.mean()) ** 252 - 1
    annualized_index_returns = (1 + index_returns.mean()) ** 252 - 1

    # Calculate annualized volatility
    annualized_strategy_volatility = strategy_returns.std() * np.sqrt(252)
    annualized_index_volatility = index_returns.std() * np.sqrt(252)

    # Calculate Sharpe ratio
    strategy_sharpe_ratio = annualized_strategy_returns / annualized_strategy_volatility
    index_sharpe_ratio = annualized_index_returns / annualized_index_volatility

    # Create a DataFrame for clear representation
    performance_metrics = pd.DataFrame({
        "Trading Strategy": [annualized_strategy_returns, annualized_strategy_volatility, strategy_sharpe_ratio],
        "Index": [annualized_index_returns, annualized_index_volatility, index_sharpe_ratio]
    }, index=["Annualized Returns", "Annualized Volatility", "Sharpe Ratio"])

    return performance_metrics

How to Use This Function

Add the above function to your MomentumStrategy class. Once implemented, you can call it to display the metrics:

metrics = trade_strategy.calculate_performance_metrics()
print(metrics)

Expected Output

A neatly formatted table summarizing the performance metrics:

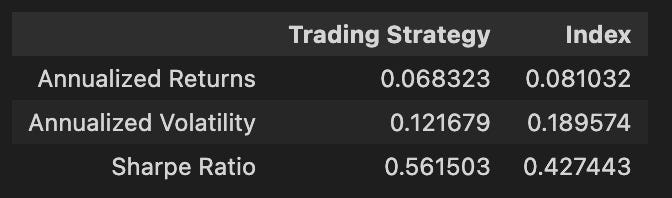
Optimizing for the Highest Sharpe Ratio

This is an exciting step where we determine the moving average period that maximizes the risk-adjusted returns, represented by the Sharpe Ratio. The process involves testing a range of moving averages to identify the one that delivers the best performance.

Implementation Steps

We use a for loop to evaluate different moving average lengths, recording the corresponding Sharpe Ratio for each. Finally, we visualize the results and identify the optimal moving average.

Code for Optimization

# Testing different moving averages to optimize for the best Sharpe Ratio
sharpe_results = []

# Loop through moving average values ranging from 10 to 5000, in increments of 10
for period in range(10, 5000, 10):
    # Initialize the Momentum class with the current moving average
    trade_strategy = Momentum(spx_close, period, 1000000, 0.001)
    trade_strategy.trade()
    # Calculate performance metrics and store the Sharpe Ratio
    metrics = trade_strategy.performance()
    sharpe_results.append([period, metrics.loc["Sharpe Ratio", "Trading Strategy"]])

# Convert results into a DataFrame
sharpe_results_df = pd.DataFrame(sharpe_results, columns=["Moving Average", "Sharpe Ratio"])

# Visualize the Sharpe Ratio across moving averages
plt.figure(figsize=(10, 5))
plt.plot(sharpe_results_df["Moving Average"], sharpe_results_df["Sharpe Ratio"], color='blue')
# Highlight the moving average with the highest Sharpe Ratio
best_ma = sharpe_results_df["Moving Average"][sharpe_results_df["Sharpe Ratio"].idxmax()]
plt.axvline(x=best_ma, color='red', linestyle='--')
plt.title("Sharpe Ratio for Different Moving Averages")
plt.xlabel("Moving Average")
plt.ylabel("Sharpe Ratio")
plt.grid()
plt.show()

# Display the optimal moving average and its Sharpe Ratio
optimal_sharpe = sharpe_results_df[sharpe_results_df["Sharpe Ratio"] == sharpe_results_df["Sharpe Ratio"].max()]
print(optimal_sharpe)

Expected Outcome

After running the above code, you will observe:

1. A line plot of Sharpe Ratios across different moving averages.

2. A vertical line highlighting the moving average with the highest Sharpe Ratio.

The console will display the specific moving average and its corresponding Sharpe Ratio.

For instance:

• Optimal Moving Average: 260 days

• Sharpe Ratio: 0.598

Insights

The optimal 260-day moving average delivers the best balance between return and risk, as indicated by its superior Sharpe Ratio. This result provides a key takeaway for refining the momentum strategy to maximize its effectiveness.